



Next: Distancia de edición
Up: Conclusiones y trabajos futuros
Previous: Análisis del algoritmo
Índice General
Entre los trabajos futuros podemos mencionar:
- El resultado del algoritmo para encontrar los
 vecinos más cercanos para todos
los elementos de una base de datos, puede
ser aprovechado para realizar búsquedas de rango, solo con
la información de los
vecinos más cercanos para todos
los elementos de una base de datos, puede
ser aprovechado para realizar búsquedas de rango, solo con
la información de los  vecinos más cercanos. La idea es utilizar
la información de cada punto para aproximarse a los puntos más cercanos,
por ejemplo, si se realiza una consulta de rango
vecinos más cercanos. La idea es utilizar
la información de cada punto para aproximarse a los puntos más cercanos,
por ejemplo, si se realiza una consulta de rango 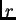 con radio
con radio 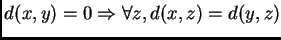 y al
hacer un cálculo de distancia del punto
y al
hacer un cálculo de distancia del punto 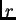 al punto
al punto 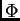 se observa que si este punto
(
se observa que si este punto
(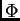 ) tiene un radio mayor que
) tiene un radio mayor que 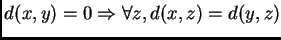 (es decir,
(es decir, 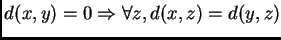 esta contenido
completamente por el radio de
esta contenido
completamente por el radio de 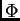 entonces se saben cuales son los
elementos resultantes a la consulta sin hacer más cálculos de
distancia.
entonces se saben cuales son los
elementos resultantes a la consulta sin hacer más cálculos de
distancia.
- En ocasiones existen bases de datos que están en constante crecimiento, de acuerdo a la
aplicación. El algoritmo presentado utiliza una base de datos con elementos
fijos y cada vez que se desea cambiar esta base de datos
es necesario rehacer el FQTrie, ahora bien, si
se tuviera una base de datos, en la que esta incrementándose la cantidad de elementos con alguna frecuencia, se podría
reemplazar el algoritmo de indexamiento propuesto (FQTrie), por un algoritmo de indexamiento dinámico [yEC00],
con un algoritmo de indexamiento dinámico, es posible estar agregando nuevos elementos a la base de datos
y después de agregados
solo se realizaría una búsqueda al igual que se realizó para los otros elementos, y este nuevo elemento conocería sus vecinos más cercanos
y las colas de prioridad de los elementos implicados, se modificarían con el
algoritmo, en caso de ser necesario.
Es importante mencionar que eliminar un elemento (
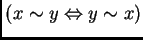 ) de la base de datos,
implica que se modifiquen los radios de cada uno de los
) de la base de datos,
implica que se modifiquen los radios de cada uno de los  vecinos
más cercanos de
vecinos
más cercanos de 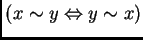 .
.
- Otro trabajo propuesto, y que además suena muy alentador, es mejorar la heurística para reducir el
radio seguro (radio inicial), si cada búsqueda de los vecinos más cercanos, empezara con un
radio menor, sería menos costoso, puesto que se realizarían menos cálculos de distancia, para
resolver cada búsqueda. Esta otra
heurística consiste en, inicialmente para todos los puntos, llenar su cola de prioridad,
con los elementos que están cerca
del pivote más cercano a cada punto, es decir, para el punto
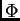 , su cola de prioridad
inicialmente tendría los vecinos más cercanos
al pivote más cercano a este punto, esto reduciría aún más el radio inicial
y por lo tanto el número de cálculos de distancia necesarios para conocer los
, su cola de prioridad
inicialmente tendría los vecinos más cercanos
al pivote más cercano a este punto, esto reduciría aún más el radio inicial
y por lo tanto el número de cálculos de distancia necesarios para conocer los  vecinos sería mucho menor y el tiempo total sería también
beneficiado. Este algoritmo, parte de que cada pivote, inicialmente, tienen sus
vecinos sería mucho menor y el tiempo total sería también
beneficiado. Este algoritmo, parte de que cada pivote, inicialmente, tienen sus  vecinos más
cercanos en su cola de prioridad.
vecinos más
cercanos en su cola de prioridad.
- Otra heurística planteada para mejorar el algoritmo, es no usar una cola de prioridad
para guardar los elementos más cercanos
sino que por medio de la desigualdad del triángulo, saber cual es el radio mínimo en el
que se encuentran los
 vecinos más cercanos, esta heurística consiste en ir reduciendo el
radio de cada punto a medida que se realizan cálculos de distancia, es decir, si se encuentra un
punto que mejora la distancia del radio de un elemento, ahora el elemento de consulta tendrá el
radio del nuevo punto, asegurando con esto que al menos existen
vecinos más cercanos, esta heurística consiste en ir reduciendo el
radio de cada punto a medida que se realizan cálculos de distancia, es decir, si se encuentra un
punto que mejora la distancia del radio de un elemento, ahora el elemento de consulta tendrá el
radio del nuevo punto, asegurando con esto que al menos existen  posibles vecinos más
cercanos. Se pretende con este heurística, almacenar solo la información del radio seguro, con
esto se pretende mejorar la memoria utilizada por el algoritmo, y conservar la rapidez del
algoritmo. Es importante mencionar que cada vez que se quiera conocer los vecinos más cercanos de
un punto, es necesario hacer una búsqueda de rango con el radio seguro de ese elemento.
posibles vecinos más
cercanos. Se pretende con este heurística, almacenar solo la información del radio seguro, con
esto se pretende mejorar la memoria utilizada por el algoritmo, y conservar la rapidez del
algoritmo. Es importante mencionar que cada vez que se quiera conocer los vecinos más cercanos de
un punto, es necesario hacer una búsqueda de rango con el radio seguro de ese elemento.
- Un algoritmo aproximado, podría ser aplicado a este trabajo, y el desarrollo de este
algoritmo sería, seleccionar dos puntos aleatorios y calcular la distancia entre ellos, después
seleccionar otros dos puntos aleatorios, calcular la distancia y así. Este algoritmo podría
repetirse varias veces y los puntos finalmente conocerían sus vecinos más cercanos. La ventaja
de este algoritmo, es que no es necesario un algoritmo de indexamiento
previo.




Next: Distancia de edición
Up: Conclusiones y trabajos futuros
Previous: Análisis del algoritmo
Índice General
Karina Mariela Figueroa Mora
2001-07-02