Un ejemplo del FQA

En esta sección se presentará un ejemplo del proceso de búsqueda en el FQA. Considere el FHFQT de la figura . Cada ramificación de la raíz representa una distancia al pivote $p_1$. Las ramificaciones de los nodos del segundo nivel se refieren a la distancia a $p_2$ y así sucesivamente.

Figura: Representación de la búsqueda en FHFQT (Fixed Height FQT)

Figura: Representación de la búsqueda en FQA (Fixed Query Array).

El equivalente FQA a partir del FHFQT de la figura guarda los elementos en el orden de izquierda a derecha, guardando las cuatro distancias para cada elemento, es decir, para llegar al elemento 1 debemos recorrer la rama de los elementos a distancia 1 y descender por esa rama, hasta las hojas, con lo cual se obtiene {1 2 5 1} (la primer línea de la tabla (a) de la figura . La figura en la tabla (a) ilustra este proceso, cabe mencionar que las tablas (b), (c), (d) representan los pasos seguidos para una búsqueda en cada nivel del FHFQT, es decir, la tabla (b) representa con negritas las ramas que serán consideradas en el siguiente paso de la búsqueda. Tenemos cuatro pivotes, y cada renglón en las cuatro tablas (a), (b), (c) y (d) representa una rama en el árbol; con la distancia de los puntos de la base de datos al pivote apropiado. Para una consulta $q$ calculamos el vector $(d(q, p_1) ... d(q, p_4))$, es decir, calculamos $d(q,p_i)$, en este caso este cálculo obtiene $(3,4,5,4)$, si radio de búsqueda es 2, tenemos que los intervalos de búsqueda son $(\{1,5\},\{2,6\},\{3,7\},\{2,6\})$ en cada nivel del árbol respectivamente, Las ramificaciones etiquetadas como en el primer nivel van a ser examinadas y, recursivamente, todas las ramificaciones con búsqueda binaria se encuentran los intervalos en la primera columna, en cada una de las cuatro tablas, mostramos a los candidatos con negritas para cada paso. 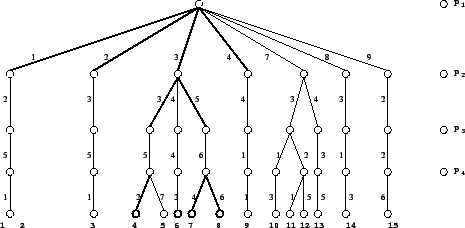La tabla $(a)$ es equivalente al primer nivel en el 7 árbol, la tabla para el segundo nivel, y así para el resto. Podemos fácilmente verificar que los intervalos para la búsqueda binaria en cada columna es equivalente a limitar la búsqueda en los niveles apropiados en el árbol.

Debe observarse que el orden lexicográfico nos permite usar la búsqueda binaria en las columnas subsecuentes. Considerando por ejemplo las columnas que empiezan con un 3: los elementos de la segunda columna son también ordenados en orden creciente y así, la figura muestra este proceso de búsqueda.

Es claro que la lista de candidatos usando cualquier representación no cambia. En la búsqueda basada en el arreglo tenemos que pagar $O(log$ $n)$ (el costo de la búsqueda binaria) para simular la visita a cada ramificación. Si visitamos $m$ nodos en el árbol, usamos $O(m$ log $n)$.