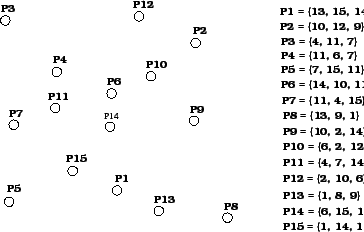
 . La cola de prioridad resultante se muestra en la figura
. La cola de prioridad resultante se muestra en la figura
En esta sección se presenta el código para las operaciones básicas de
la cola de prioridad las cuales son insertar, borrar.
La operación de la cola de prioridad insertar agrega elementos a
la cola de prioridad, manteniendo la condición de la cola de
prioridad en todos los lugares. Esta operación incrementan en uno el tamaño de
la cola de prioridad
( debe ser incrementado). El registro a ser insertado es puesto en , pero esto podría violar
la propiedad de la cola de prioridad. Si la propiedad de la cola de prioridad es violada (el nuevo nodo es mayor que sus padres),
entonces la violación puede ser terminada intercambiando el nuevo nodo con su padre. Esto puede,
en su momento, causar una violación, y esto puede ser solucionado de la misma manera. Por ejemplo,
si es insertado en la cola de prioridad de la figura ![]() , esto es primero guardado en
como el hijo derecho de . Entonces, como es mayor que , se intercambia con este, y
como es mayor que , también se intercambia con este, y el proceso termina porque es
menor que
, esto es primero guardado en
como el hijo derecho de . Entonces, como es mayor que , se intercambia con este, y
como es mayor que , también se intercambia con este, y el proceso termina porque es
menor que  . La cola de prioridad resultante se muestra en la figura
. La cola de prioridad resultante se muestra en la figura ![]() .
.
El código para el método insertar es hacia arriba. En la siguiente implementación, agregamos un nuevo elemento a , entonces llamamos a para romper las violaciones a la condición de la cola de prioridad.
upheap(int k)
{
int v;
v = a[k]; a[0] = INTMAX;
while (a[k/2] v)
{
a[k] = a[k/2]; k = k/2;
}
a[k] = v;
}
insertar(int v)
{
a[++N] = v;
upheap(N);
}
Una llave centinela debe ser puesta en para detener el ciclo para el caso que es mayor que
todas las llaves en la cola de prioridad.
La operación remover el más grande envuelve casi el mismo proceso, la figura
![]() muestra el resultado de remover
muestra el resultado de remover  de la cola de prioridad, como puede observarse, el
último elemento de la cola de prioridad se coloca en el lugar del primer elemento, es decir se coloca en
lugar de
de la cola de prioridad, como puede observarse, el
último elemento de la cola de prioridad se coloca en el lugar del primer elemento, es decir se coloca en
lugar de  , y ahora se hace un recorrido hacia abajo hasta que todos los elementos de
la cola de prioridad
cumplan con la propiedad de este.
, y ahora se hace un recorrido hacia abajo hasta que todos los elementos de
la cola de prioridad
cumplan con la propiedad de este.
El código para realizar esta operación se muestra a continuación, como puede observarse, ahora el proceso debe ser hacia abajo, y N debe disminuirse en 1.
downheap(int k)
{
int j,v;
v = a[k];
while ( k N/2)
{
j = k + k;
if(j![]() N
N ![]() a[j]
a[j] ![]() a[j+1]) j++;
a[j+1]) j++;
if(v  a[j]) break;
a[j]) break;
a[k] = a[j]; k = j;
}
a[k] = v;
}
remover()
{
int v = a[1];
a[1] = a[N-];
downheap(N);
return v;
}