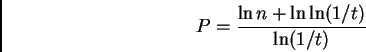Implementación de dos colas de prioridad

En esta sección se presenta una implementación de una doble cola de prioridad [MDAS98]. El propósito de esta estructura, llamada Min-Max heap, es que puede ser construida en tiempo lineal, en contraste con las colas de prioridad convencionales, este permite encontrar el elemento mínimo y el elemento máximo, las operaciones de insertar, remover mínimo, remover el máximo, encontrar mínimo, encontrar máximo pueden ser desarrolladas en tiempo logarítmico.

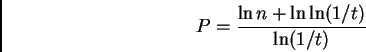Esta cola de prioridad se define como sigue. Dado un conjunto $S$ de valores, un cola de prioridad min-max sobre $S$ es un árbol binario $T$ con las siguientes propiedades.

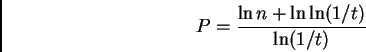1. $T$ tiene la forma de una cola de prioridad
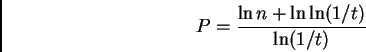2. $T$ esta ordenado min-max $\colon$ los valores guardados en los nodos en los niveles pares (pueden ser los nones) son menores que los valores guardados en sus descendientes, donde la raíz es el nivel cero. Entonces el valor menor es guardado en uno de los hijos raíz, un ejemplo de una cola de prioridad min-max se muestra en la figura .

Figura: Ejemplo de una cola de prioridad min-max. La condición de la cola de prioridad alterna entre el mínimo y máximo de nivel a nivel

Una cola de prioridad min-max de elementos pueden ser ordenados en un arreglo $A[1...N]$. La localidad $i$th en el arreglo puede corresponder a un nodo localizado en el nivel $\lfloor (log_2$ $i)\rfloor$ en la cola de prioridad. Un heap min-max es definido análogamente; como una cola de prioridad, el valor máximo esta guardado en la raíz, y el valor mínimo esta guardado en uno de los hijos de la raíz.

Es interesante observar el diagrama de Hasse para una cola de prioridad min-max el cual mucho más complejo en contraste con una cola de prioridad tradicional. La figura muestra el diagrama de Hasse para la figura .

Figura B.5: Diagrama de Hasse para la cola de prioridad min-max de la figura

El procedimiento para el algoritmo de la cola de prioridad min-max es muy similar a su correspondiente cola de prioridad convencional. La cola de prioridad tradicional es construido hacia arriba y hacia abajo. Cuando el algoritmo examina el subárbol de $A[i]$ entonces ambos subárboles de $A[i]$ son max-ordenados, mientras que el subárbol por sí mismo no puede no ser necesariamente ordenado. El paso TrickleDown de este algoritmo intercambia los valores de $A[i]$ con el máximo de sus hijos. Este paso es entonces aplicado recursivamente a su hijo máximo para mantener el max-orden. En la cola de prioridad min-max, el orden requerido debe ser establecido entre un elemento sus hijos y su nietos. El procedimiento diferencia entre los niveles min y max. La descripción de este procedimiento es el siguiente.

procedure TrickleDown(i) 

$i$ es la posicion en el arreglo

if $i$ esta en un nivel min then


TrickleDownMin(i)

else


TrickleDownMax(i)

endif



procedure TrickleDownMin(i) 

if A[i] tiene hijos then


m:= indice del mas pequeño de los hijos y los nietos (si hay) de A[i] 

if A[m] es un nieto de A[i] then 

if A[m] $<$ A[i] then 


swap A[i] y A[m] 

if A[m]  A[parent(m)] then 


swap A[m] y A[parent(m]] 

endif 


TrickleDownMin(m) 

endif   

else { A[m] es un hijo de A[i] }

if A[m] $<$ A[i] then 


swap A[i] y A[m] 

endif 

endif 

El procedimiento TrickleDownMax es el mismo excepto que los operadores relacionales están invertidos. Las operaciones de DeleteMin y DeleteMax son análogas a borrar en una cola de prioridad convencional. Específicamente, los elementos requeridos son extraídos y la posición vacante es llenada con el ultimo elemento de la cola de prioridad. El orden min-max es mantenido después de aplicar el procedimiento TrickleDown.